BaseCrossドキュメント(2017年)

０１０．立方体とライティング(Dx11版)

　このサンプルはSimplSample010というディレクトリに含まれます。
　BaseCrossDx11.slnというソリューションを開くとDx11版が起動します。

　実行結果は以下のような画面が出ます。

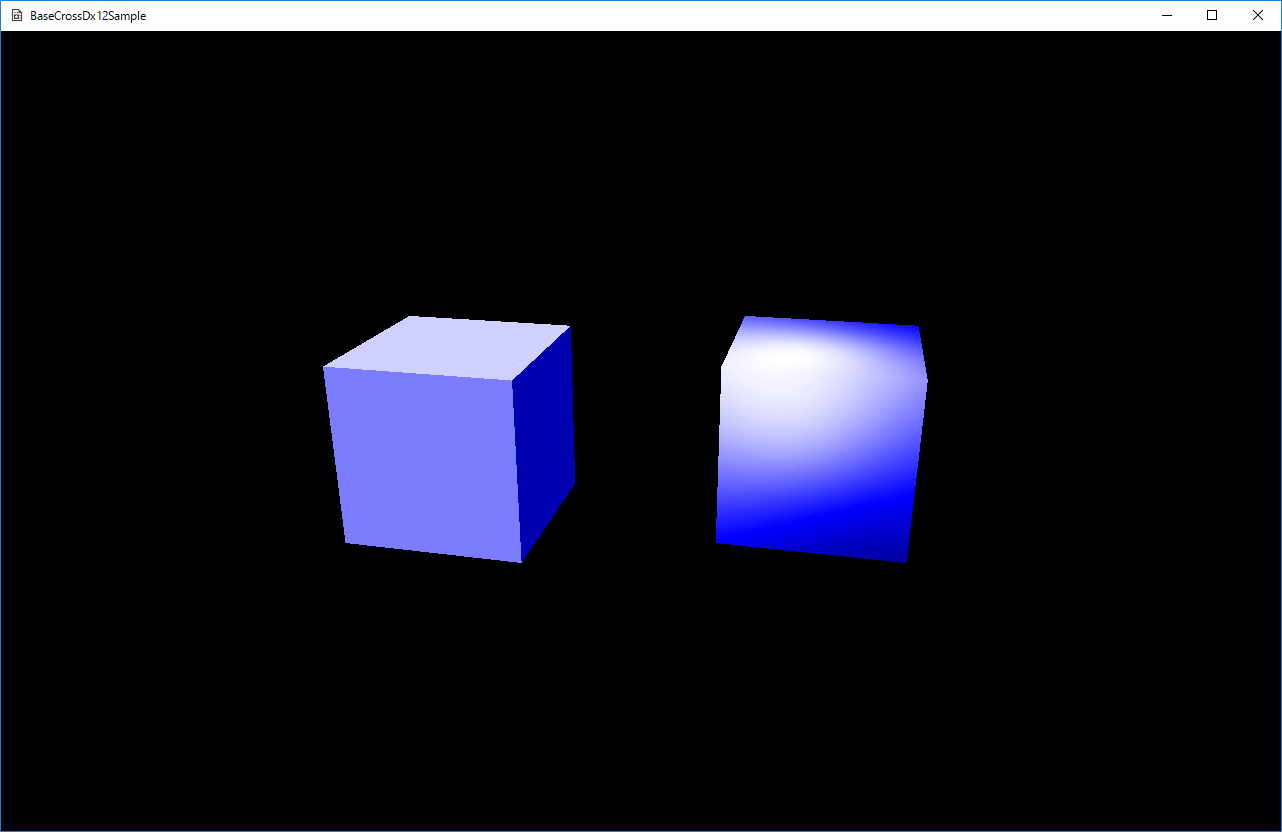
図0010a

　動画は以下になります。

【サンプルのポイント】

　今項でのテーマはライティングです。３Ｄ表現でなくてはならない処理です。ライティングによって、オブジェクトに陰（影ではありません）を表示できます。　ライティングを実装するためには頂点に法線の情報を入れる必要があります。どのように法線を入れるかで、どのようなライティングになるかが変わります。このサンプルでは、その違いを確認しましょう。

【共通解説】

　Dx12、Dx11両方に共通なのはシェーダーです。DxSharedプロジェクト内にシェーダファイルというフィルタがあり、そこに記述されてます。
　今回使用するシェーダは頂点シェーダとピクセルシェーダです。VertexPositionNormal型の頂点を持つものです。コンスタントバッファもあります。
　今回のポイントはライティングです。ですので、そこに絞って説明します。以下は頂点シェーダですVSPNStatic.hlslにあります。抜粋（main関数のみ）ですが、

PSPNInput main(VSPNInput input)
{
    PSPNInput result;
    //頂点の位置を変換
    float4 pos = float4(input.position.xyz, 1.0f);
    //ワールド変換
    pos = mul(pos, World);
    //ビュー変換
    pos = mul(pos, View);
    //射影変換
    pos = mul(pos, Projection);
    //ピクセルシェーダに渡す変数に設定
    result.position = pos;
    //ライティング
    result.norm = mul(input.norm, (float3x3)World);
    result.norm = normalize(result.norm);
    return result;
}

　赤くなっているところが、頂点シェーダにおけるライティングです。
　これの意味するところは、4X4行列の3X3の部分だけ取り出すという意味です。これはスケーリングと回転のみ取り出すということです。
　もともと頂点シェーダに渡される法線は原点を中心とした立方体に対する法線です。これをワールド変換によって、スケーリングと回転、そして移動がなされるわけですが、移動の要素は、ライトが平行ライトなので、どの場所でもライトの向きは一緒です。ですから、ワールド行列のスケーリングと回転をもとに、渡された法線を変換してあげればよいのです。
　するとワールド変換された法線が計算できます。法線なので正規化もしています。
　そして以下はピクセルシェーダです。PSPNStatic.hlslです。同様main関数のみですが、

float4 main(PSPNInput input) : SV_TARGET
{
    //法線ライティング
    float3 lightdir = normalize(LightDir.xyz);
    float3 N1 = normalize(input.norm);
    float4 Light = saturate(dot(N1, -lightdir) * Diffuse + Emissive);
    Light.a = Diffuse.a;
    return Light;
}

　赤くなっているところがポイントですが、以下の図を見てください。

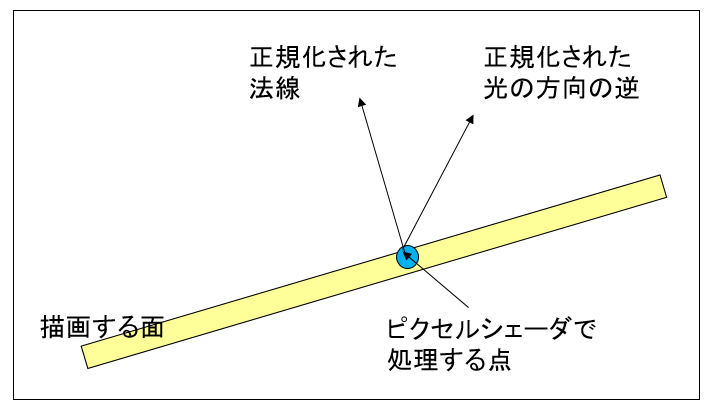
図0010b

　この図は、通常描画（フラットではない）の場合の、ピクセルシェーダに渡される法線と、ライトの関係を示したものです。両方とも正規化されているとします。ピクセルシェーダではその表面の1つの点を処理するので、青い丸のところだけ考えます。
　法線とライトから、この点の明るさを求めればいいことがわかります。
　続いて以下の図を見てください。

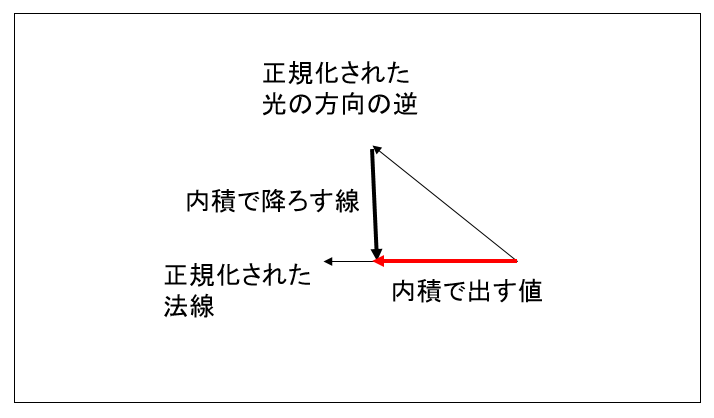
図0010c

　この図は前の図から正規化された法線と正規化された光の方向の逆の関係を示したものです。正規化された法線に対して正規化された光の方向の逆の内積を出すと、赤い線の長さが出せるのがわかります。また、それは最高で1.0であり（法線とライトが重なっている場合）、最低で0.0です（法線とライトが90度になってる場合）。
　このことから

    float4 Light = dot(N1, -lightdir);

　という計算ができるのがわかります。
　一般的にデフューズは掛け算で、エミッシブは足し算ですから

    float4 Light = dot(N1, -lightdir) * Diffuse + Emissive;

　が導けます。ただ、この計算ではLightの各値が1.0を超える場合もあるので、ピクセルシェーダのリターンはカラーを返すので、saturate()関数によって、0から1.0までの間に丸めます。
　そして最終的に、アルファ値（デフィーズのアルファを使う）を設定し、リターンします。

【Dx11版解説】

　BaseCrossDx11.slnを開くと、BaseCrossDx11というメインプロジェクトがあります。この中のCharacter.h/cppが主な記述個所になります。

■初期化■

　主な初期化は頂点の初期化です。ここではフラットライティング用の頂点と面にライティング用の頂点を作成します。
　以下はCubeObject::CreateBuffers()関数ですが

void CubeObject::CreateBuffers() {
    float HelfSize = 0.5f;
    vector<Vec3> PosVec = {
        { Vec3(-HelfSize, HelfSize, -HelfSize) },
        { Vec3(HelfSize, HelfSize, -HelfSize) },
        { Vec3(-HelfSize, -HelfSize, -HelfSize) },
        { Vec3(HelfSize, -HelfSize, -HelfSize) },
        { Vec3(HelfSize, HelfSize, HelfSize) },
        { Vec3(-HelfSize, HelfSize, HelfSize) },
        { Vec3(HelfSize, -HelfSize, HelfSize) },
        { Vec3(-HelfSize, -HelfSize, HelfSize) },
    };
    vector<UINT> PosIndeces = {
        0, 1, 2, 3,
        1, 4, 3, 6,
        4, 5, 6, 7,
        5, 0, 7, 2,
        5, 4, 0, 1,
        2, 3, 7, 6,
    };


    vector<Vec3> FaceNormalVec = {
        { Vec3(0, 0, -1.0f) },
        { Vec3(1.0f, 0, 0) },
        { Vec3(0, 0, 1.0f) },
        { Vec3(-1.0f, 0, 0) },
        { Vec3(0, 1.0f, 0) },
        { Vec3(0, -1.0f, 0) }
    };

    vector<VertexPositionNormal> vertices;
    vector<uint16_t> indices;
    UINT BasePosCount = 0;
    for (int i = 0; i < 6; i++) {
        for (int j = 0; j < 4; j++) {
            VertexPositionNormal Data;
            Data.position = PosVec[PosIndeces[BasePosCount + j]];
            if (m_Flat) {
                //フラット表示の場合は法線は頂点方向にする
                Data.normal = Data.position;
                Data.normal.normalize();
            }
            else {
                //フラット表示しない場合は、法線は面の向き
                Data.normal = FaceNormalVec[i];
            }
            vertices.push_back(Data);
        }

        indices.push_back((uint16_t)BasePosCount + 0);
        indices.push_back((uint16_t)BasePosCount + 1);
        indices.push_back((uint16_t)BasePosCount + 2);
        indices.push_back((uint16_t)BasePosCount + 1);
        indices.push_back((uint16_t)BasePosCount + 3);
        indices.push_back((uint16_t)BasePosCount + 2);

        BasePosCount += 4;
    }

    //メッシュの作成（変更できない）
    m_CubeMesh = MeshResource::CreateMeshResource(vertices, indices, false);
}

　順を追って説明しますと、まず、元になる頂点の配列とインデックスの配列を作成します。以下の部分です。

    float HelfSize = 0.5f;
    vector<Vec3> PosVec = {
        { Vec3(-HelfSize, HelfSize, -HelfSize) },
        { Vec3(HelfSize, HelfSize, -HelfSize) },
        { Vec3(-HelfSize, -HelfSize, -HelfSize) },
        { Vec3(HelfSize, -HelfSize, -HelfSize) },
        { Vec3(HelfSize, HelfSize, HelfSize) },
        { Vec3(-HelfSize, HelfSize, HelfSize) },
        { Vec3(HelfSize, -HelfSize, HelfSize) },
        { Vec3(-HelfSize, -HelfSize, HelfSize) },
    };
    vector<UINT> PosIndeces = {
        0, 1, 2, 3,
        1, 4, 3, 6,
        4, 5, 6, 7,
        5, 0, 7, 2,
        5, 4, 0, 1,
        2, 3, 7, 6,
    };

　元になる頂点は、ローカル上の頂点ですから、各XYZ軸にHelfSizeずつ、プラス方向かマイナス方向に伸ばした位置です。
　立方体ですから、8個の頂点になります。ここで、元になると言っているのは、この頂点と実際にメッシュに作成する頂点は違いますので、気を付けましょう。
　続いて、各面の法線を作成します。ライティングするためには、各頂点の法線を指定しなければいけません。立方体のように角張ったオブジェクトを描画するためには面に対する法線を各頂点に設定します。しかしフラットな描画や球のような滑らかなオブジェクトの場合は、法線は面に対するものではなく頂点の方向で設定します。以下が面に対する法線を作成しているところです。面は6つですから、6個の配列になります。

    vector<Vec3> FaceNormalVec = {
        { Vec3(0, 0, -1.0f) },
        { Vec3(1.0f, 0, 0) },
        { Vec3(0, 0, 1.0f) },
        { Vec3(-1.0f, 0, 0) },
        { Vec3(0, 1.0f, 0) },
        { Vec3(0, -1.0f, 0) }
    };

　ここまでで、メッシュを作成するための材料がそろいました。それで、実際にメッシュを作成します。フラット描画の場合と通常描画の場合で作成方法が違いますので注意しましょう。

    vector<VertexPositionNormal> vertices;
    vector<uint16_t> indices;
    UINT BasePosCount = 0;
    for (int i = 0; i < 6; i++) {
        for (int j = 0; j < 4; j++) {
            VertexPositionNormal Data;
            Data.position = PosVec[PosIndeces[BasePosCount + j]];
            if (m_Flat) {
                //フラット表示の場合は法線は頂点方向にする
                Data.normal = Data.position;
                Data.normal.normalize();
            }
            else {
                //フラット表示しない場合は、法線は面の向き
                Data.normal = FaceNormalVec[i];
            }
            vertices.push_back(Data);
        }

        indices.push_back((uint16_t)BasePosCount + 0);
        indices.push_back((uint16_t)BasePosCount + 1);
        indices.push_back((uint16_t)BasePosCount + 2);
        indices.push_back((uint16_t)BasePosCount + 1);
        indices.push_back((uint16_t)BasePosCount + 3);
        indices.push_back((uint16_t)BasePosCount + 2);

        BasePosCount += 4;
    }

    //メッシュの作成（変更できない）
    m_CubeMesh = MeshResource::CreateMeshResource(vertices, indices, false);

　ここで、verticesとindicesという2つの配列を初期化して、最後にMeshResource::CreateMeshResource()関数呼び出しでメッシュを作成します。
　外側のforループでは6つの面をループします。

    //6つの面のループ
    for (int i = 0; i < 6; i++) {

　内側のループは各頂点のループです。1つの面を作成するのに4つの頂点が必要ですから4回ループします。

        for (int j = 0; j < 4; j++) {

　そしてこのループ内で、vertices配列に追加する頂点を決定します。

            VertexPositionNormal Data;
            Data.position = PosVec[PosIndeces[BasePosCount + j]];

　上記の2行は、どの元になる頂点のデータを使うかを決定しています。PosVec及びPosIndeces配列の中身がどうなっているか再確認しながら追いかけていくと理解できると思います。
　続いてフラットかそうでないかにより法線が決定します。

            if (m_Flat) {
                //フラット表示の場合は法線は頂点方向にする
                Data.normal = Data.position;
                Data.normal.normalize();
            }
            else {
                //フラット表示しない場合は、法線は面の向き
                Data.normal = FaceNormalVec[i];
            }

　フラットの場合の

                //フラット表示の場合は法線は頂点方向にする
                Data.normal = Data.position;
                Data.normal.normalize();

　に、あれと思うかもしれません。これは、ローカルの立方体が、原点を中心に作成されているので、Data.positionがそのまま法線の向きになるのです。ですから

                //フラット表示の場合は法線は頂点方向にする
                Data.normal = Data.position - Vec3(0,0,0);

　と同じ意味です。原点を引き算するのと同じです。
　フラットではない場合は面の法線テーブルから法線をとってきて代入します。
　最後に、

    //メッシュの作成（変更できない）
    m_CubeMesh = MeshResource::CreateMeshResource(vertices, indices, false);

　とメッシュを作成します。
　さて、このメッシュ作成の場合、フラットの場合は、頂点が余分にあるのがわかると思います。ある頂点の法線は、原点の逆方向に向くので、同じ内容の頂点が3つずつ出てきます。ですから、フラット描画が決定しているのであれば、メッシュを作成するときの頂点を減らすことができます。しかしその場合、頂点情報の変更する場合は注意が必要です。例えば場合によってフラット描画かそうでないかを切り替えて描画する場合は、上記のように余分な頂点を作成しておいてもいいと思います（立方体の場合、トータルの頂点数もそんなに多くないので）。

■更新処理■

　CubeObject::OnUpdate()関数です。オブジェクトを回転させています。

■描画処理■

　前項の描画と同様ですが。コンスタントバッファに渡すデフィーズとエミッシブの値に注目しましょう。

【まとめ】

　今回はライティングと法線の関係について法線を変えて頂点を作成するという方法で紹介しました。描画そのものは前項とシェーダと頂点型こそ違いうますが、処理は同じような感じです。

０．シンプルバージョンサンプル(Dx11版)